机器学习笔记

在读吴军的《智能时代》和《数学之美》时常常被技术的力量给震撼到，尤其是其中现实的例子特别具有说服力，未来的发展或许由人工智能驱动。当然在深度方面，自学肯定不如专科博士生，不过未来人工智能或许就像现在的编程一样成为一种基础工具。今年的计划之一就是学习人工智能，因为离开学习太久，学习理论的东西不如从前。这一篇指南 如何用3个月零基础入门「机器学习」 提供的建议非常受用。目前在看 吴恩达的 《机器学习》视频，已完成监督学习部分，这儿做一个阶段性复习。

这个视频所涉及到的理论知识很少，不过跟着练习做完也发现已经可以解决很多问题了。首先是机器学习分为监督学习和非监督学习。监督学习就是已知训练数据集的结果，对未来的一些数据进行预测，比如数字识别，邮件分类，房价预测。非监督学习就是我们不知道结果，比如推荐系统中发现同时购买的商品。

线性回归

单一特征参数

线性回归大家应该都已经使用过，记得大学做物理实验的时候需要根据收集到的数据找到实验变量直接的线性关系，实验中的数据处理很多用的就是最小二乘法。假设收集到的数据已经打点在坐标系上，要求的一元线性回归方程形如 y = ax + b，我们需要保证这个直线离所有的点尽可能的近。

这个课程给的例子是已知房屋面积和价格的一组数据，我们需要找到它们之间的关系以便我们预测房价。我们可以把假设函数定义为

$$h_\theta(x) = \theta_0 + \theta_1x$$

为了评估我们的函数模型，我们引入损失函数（Cost Function）（其中的 $\hat{y_i}$ 是预测值）：

$$J(\theta_0, \theta_1)=\frac{1}{2m}\sum_{i = 1}^{n}(\hat{y_i} - y_i)^2 = \frac{1}{2m}\sum_{i = 1}^{n}(h_θ(x_i) - y_i)^2$$

我们希望这个损失函数结果越小越好（最小二乘法），也就是求它的最小值。我们可以先回顾一下一元函数的极值求法，之前讲求根运算时介绍过牛顿迭代法，我们的递归式

$$x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)}$$

图形化的解释：

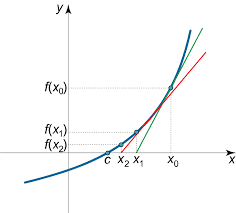
初始迭代的点为 $x_0$，之后根据斜率和 $f(x_0)$ 计算第二个点 $x_1$，一直到斜率趋于 0。斜率的正负决定了收敛方向，斜率的大小决定了收敛的速度。再来看下梯度下降，简单来说我们只需要将 $f(x_0)$ 替换为一个常量 $\alpha$ 比如 0.03。 比较而言，牛顿法具有很好的收敛性，而梯度下降要简单一些。下面是使用梯度下降找到极值的直观例子，就像沿着山坡最陡峭的方向往下走。

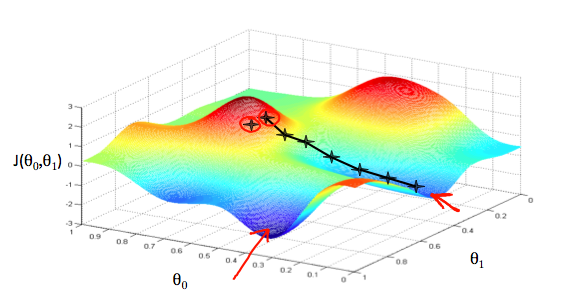
从图上可以看出，我们求得的极值是局部最优可能不是全局最优的，这跟我们的初始值有关，不过这个不是问题。多元函数使用的是偏导，对于上面的损失函数，我们的递归式就是形如：

$$\theta_0 := \theta_0 - \alpha \frac{\partial }{\partial \theta_0}J(\theta_0, \theta_1) \\
\theta_1 := \theta_1 - \alpha \frac{\partial }{\partial \theta_1}J(\theta_1, \theta_1)$$

一直迭代下去直到偏导趋于 0，因为极值点偏导为 0。其中 $\alpha$ 的选择不能太大，太大可能导致无法收敛，太小的话迭代次数较多。注意上面的计算需要同时计算，对比下上面牛顿法的迭代式，左侧的 $\theta_0$ 和 $\theta_1$ 是第 $n + 1$ 的 $\theta$ 而 $\theta_0$ 和 $\theta_1$ 是第 n 次的 $\theta$。

接下来就是求偏导了:

$$\begin{aligned}
\frac{\partial }{\partial \theta_j}J(\theta_0, \theta_1) &= \frac{\partial }{\partial \theta_j}\frac{1}{2}(h_θ(x_i) - y_i)^2 \\
&= (h_θ(x_i) - y_i)\frac{\partial }{\partial \theta_j}(h_θ(x_i) - y_i) \\
&= (h_θ(x_i) - y_i)\frac{\partial }{\partial \theta_j}h_θ(x_i)
\end{aligned}$$

对于 $\frac{\partial }{\partial \theta_j}h_θ(x_i)$，当 $\theta_j$ 为 $\theta_0$ 时值为 1，当 $\theta_j$ 为 $\theta_1$ 时值为 x。

多元线性回归

上面的例子只有一个特征参数，实际当中的特征参数会有很多，这儿就扩展一下。

$$h_\theta(x) = \theta_0x_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + … + \theta_nx_n$$

其中 $x_0$ 始终为 1。我们又可以将上面的假设函数写成向量的形式：

$$h_\theta(x) = \left [ \begin{matrix} \theta_0 \\
\theta_1 \\ \theta_2 \\ … \\ \theta_n \end{matrix} \right ]
\left [ \begin{matrix} x_0 & x_1 & x_2 & … & x_n \end{matrix} \right ] = \theta^TX$$

损失函数为：

$$J(\theta) = \frac{1}{2m}\sum_{i = 1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2 = \frac{1}{2m}\sum_{i = 1}^{m}(\theta^Tx^{(i)} - y^{(i)})^2$$

其中 $x^{(i)}$ 和 $y^{(i)}$ 对应第 i 组数据。

偏导

$$\frac{\partial }{\partial \theta_j}J(\theta) = \frac{1}{m}\sum_{i = 1}^{m}(\theta^Tx^{(i)} - y^{(i)})x_{j}^{(i)}$$

上面的假设只是多元一次函数，其实假设函数式可以为任意多项式形式。以上面例子，我们可以把 $x_1^2$ 当成一个新的特征 $x_2$来看待。

$$h_\theta(x) = \theta_0x_0 + \theta_1x_1 + \theta_2x_1^2 + … + \theta_nx_n$$

特征缩放

上面房价的例子中，房屋的面积范围是 100 - 1000 这取决于实际数据，而我们通常选择的步长参数 $\alpha$ 是比较小的一个数。这种情况下为了减少迭代次数，我们可以把已有的数据映射到 [-1, 1] 这个范围内。

$$x_i := \frac{x_i - u_i}{s_i}$$

其中 $u_i$ 为第 i 个特征的平均值，$s_i$ 为第 i 个特征的范围。

Normal equation

梯度下降是求解 $\theta$ 的一种方式，我们要求解的 $\theta$ 满足

$$X\theta = y$$

我们可以用 求解线性方程的方式求得 $\theta$，因为 $X$ 不一定是方阵，我们需要两边同时先乘以 $X^T$

$$X^TX\theta = X^Ty$$

然后两边同时乘以 $X^TX$ 的逆矩阵，有

$$\theta = (X^TX)^{-1}X^Ty$$

如果特征矩阵不可逆，可能是存在冗余特征或者是样本太少特征太多。

矩阵求逆的时间复杂度为 $O(n^3)$ 在特征数比较少（比如小于 1000）的时候比较有优势。

上面这些就是线性回归的内容，现在就可以使用它解决房价预测的问题了。

逻辑回归

还有一个常见问题是分类问题，比如判断肿瘤是恶性还是良性，垃圾邮件分类。这类问题明显不能使用线性回归解决，假设函数 $h_\theta(x)=\theta^TX$ 结果可以是任意值，而实际值 y 只可能为 0 或 1。所以，我们必须确保假设函数 $h_\theta(x)$ 满足 $0 \leq h_\theta(x) \leq 1$。我们引入 Sigmoid 函数

$$g(z) = \frac{1}{1 + e^{-z}}$$

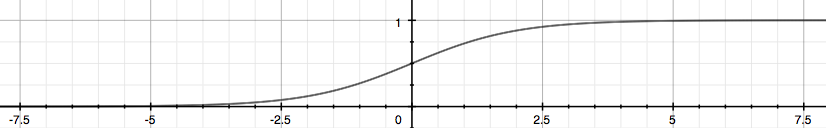
假设函数为

$$h_\theta(x)=g(\theta^TX)$$

假设函数表示的意义是 y = 1 的可能性。可以表示为

$$h_\theta(x) = P(y = 1|x;\theta) = 1 - P(y = 0|x;\theta)$$

一般来说，当 $h_\theta(x) \geq 0.5$ 时 y 为 1，当 $h_\theta(x) < 0.5$ 时 y 为 0。也就是当 $\theta^TX \geq 0$ 时 y 为 1，当 $\theta^TX < 0$ 时 y 为 0。如图所示，在我们对样本分类时，其实就是在找到一条线，将其划分为两部分，在直线下方的小于 0，在直线上方的 大于 0 。当然上面也已经提到过，我们的假设函数可以是任意多项式的函数，不一定是一条直线。

损失函数

这儿不能使用线性规划的损失函数，因为得到的不是凸函数。下面是我们的损失函数
$$J(\theta) = \frac{1}{m}\sum_{i = 1}^{m}Cost(h_θ(x^{(i)}), y^{(i)})$$
其中当 y = 0 时 $Cost(h_\theta(x), y) = -log(1 - h_\theta(x))$；当 y = 1 时，$Cost(h_\theta(x), y) = -log(h_\theta(x))$。损失函数的效果是当实际值 y 与 计算值相同时，损失为 0，如果相反则趋于无穷大。因为 y 要么为 0 要么为 1，损失函数也可以写成
$$Cost(h_\theta(x), y) = -ylog(h_\theta(x)) - (1 - y)log(1 - h_\theta(x))$$

完整的损失函数为

$$J(\theta) = \frac{1}{m}\sum_{i = 1}^{m}\left [ -y^{(i)}log(h_\theta(x^{(i)})) - (1 - y^{(i)})log(1 - h_\theta(x^{(i)})) \right ]$$

对应的偏导

$$\frac{\partial }{\partial \theta_j}J(\theta) = \frac{1}{m}\sum_{i = 1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_{j}^{(i)}$$

看上去和线性回归的很相似，这儿不再证明。

最后，如果目标分类大于 2 种，我们只需要每次分出一种，把其它的看作一类即可。

正则化和过拟合问题

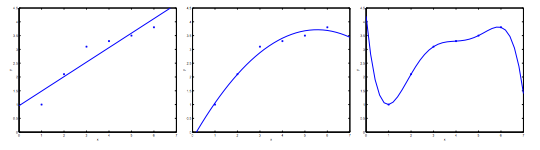
假设我们有一组数据，数据的分布如图所示，我们可以大概看出它应该是一条曲线，左侧的图表示我们在用直线来拟合这个函数，可以看出不太合适，我们称之为欠拟合。同样的道理，右侧我们使用的是一个高阶的函数来拟合，虽然曲线穿过了所有的点，但是我们知道这样的函数不具有普适性，我们称之为过拟合。

对于过拟合来说，除了减少参数，还可以使用正则化的方式。简单来说就是，我们希望保留一些特征参数，但是又不希望它的权重太重。我们在损失函数中加入惩罚项，注意我们并不惩罚 $\theta_0$ 所以， j 是从 1 开始的。

$$J(\theta) = \frac{1}{2m}\sum_{i = 1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j = 1}^{n}\theta_j^2$$

总之，我们需要求得损失函数的最小值，所以不难理解当 $\lambda$ 比较大时，$\theta$ 会非常而趋于 0。

正则化的线性回归递归式（当然 $\theta_0$ 不变）

$$\theta_j := \theta_j(1 - \alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i = 1}^{m}(h_θ(x^{(i)}) - y^{(i)})x_j^{(i)}$$

对于 Normal Equation 来说，变为

$$\theta = (X^TX + \lambda \cdot L)^{-1}X^Ty$$

其中 L 类似单位矩阵，只不过第一个位置的元素为 0 。

神经网络

神经网络的表示

神经网络的模型非常直观，一般的表示为：

Layer 1 是输入层，Layer3 是输出层，中间的是隐藏层。 隐藏层节点又称为激活单元，第 j 层的 i 个单元记为 $a_i^{(j)}$。$Θ^{(j)}$ 表示第 j 层到 j + 1 层的映射矩阵。对于上图中的节点有：
$$\begin{aligned}
a_1^{(2)} &= g(\Theta_{10}^{(1)} x_0 + \Theta_{11}^{(1)} x_1) + \Theta_{12}^{(1)} x_2 + \Theta_{13}^{(1)} x_3) \\
a_2^{(2)} &= g(\Theta_{20}^{(1)} x_0 + \Theta_{21}^{(1)} x_1) + \Theta_{22}^{(1)} x_2 + \Theta_{23}^{(1)} x_3) \\
a_3^{(2)} &= g(\Theta_{30}^{(1)} x_0 + \Theta_{31}^{(1)} x_1) + \Theta_{32}^{(1)} x_2 + \Theta_{33}^{(1)} x_3) \\
h_{\Theta}(x) = a_1^{(3)} &= g(\Theta_{10}^{(2)} a_0^{(2)} + \Theta_{11}^{(2)} a_1^{(2)}) + \Theta_{12}^{(2)} a_2^{(2)} + \Theta_{13}^{(1)} a_3^{(2)})
\end{aligned}$$

上式中在每一层都会加入第 0 项。更一般化的等式可以写成

$$z^{(j)} = \Theta^{(j-1)}a^{(j-1)}$$
$$a^{(j)} = g(z^{(j)})$$

整个来看，如果没有隐藏层的话和之前接触的模型并无不同，更多层模型可以应对更为复杂的模型。具体的应用例子是以逻辑 XNOR 为例

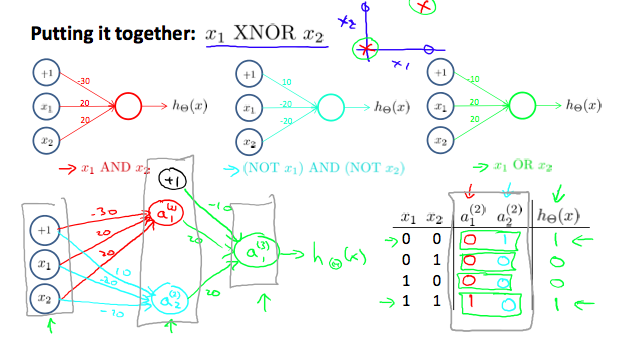
可以看出如果没有隐藏节点的话，是不能直接实现想要的逻辑功能的，更多的隐藏层和隐藏节点意味着更为复杂的模型函数。现在，还是比较容易理解隐藏节点的增加可以使模型更能够拟合现实数据。剩下的问题就是如何确定这些隐藏节点的参数。

后向传播

首先需要定义损失函数 Cost Function，我们约定网络总层数为 L，$s_l$ 为第 l 层的节点数目，K 为输出节点数目。因为神经网络的输出可能有多个节点，$h_{\Theta}(x)_k$ 为第 k 个输出的假设函数。回忆下逻辑回归的损失函数为

$$J(\theta) = \frac{1}{m}\sum_{i = 1}^{m}\left [ -y^{(i)}log(h_\theta(x^{(i)})) - (1 - y^{(i)})log(1 - h_\theta(x^{(i)})) \right ] + \frac{\lambda}{2m}\sum_{j = 1}^{n}\theta_j^2$$

神经网络对应的损失函数略微复杂，只是因为输出节点可能为多个，另外需要将所有的参数都加入惩罚项：

$$J(\Theta) = \frac{1}{m}\sum_{i = 1}^{m}\sum_{k = 1}^{K}\left [ -y_k^{(i)}log(h_{\Theta}(x^{(i)})(k)) - (1 - y_k^{(i)})log(1 - h_{\Theta}(x^{(i)}(k))) \right ] + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j = 1}^{s_{l+1}}(\Theta_{j,i}^{(l)})^2$$
同样的，我们的目的也是求其最小值。过程时这样的：
给定训练集 ${(x^{(1)}, y^{(1)})\cdot \cdot \cdot (x^{(m)}, y^{(m)})}$
初始化 $\Delta_{i,j}^{l} := 0$
对每个训练数据 t 从 1 到 m：

1. 令 $a^{(1)} := x^{(t)}$
2. 使用前向传播计算 $a^{(l)}$ l = 2,3,…,L
3. 使用 $y^{(i)}$ 计算 $\delta^{L} = a^{(L)} - y^{(L)}$
4. 计算 $\delta^{(L - 1)},\delta^{(L - 2)},….,\delta^{(2)}$
5. $\Delta_{i,j}^{l} := \Delta_{i,j}^{l} + a_j^{(l)}\delta_i^{(l + 1)}$

最后再更新 $\Delta$ 矩阵
$D_{i,j}^{(l)} := \frac{1}{m}(\Delta_{i,j}^{l} + \lambda\Theta_{i,j}^{(l)})$ 当 j != 0
$D_{i,j}^{(l)} := \frac{1}{m}\Delta_{i,j}^{l}$ 当 j = 0

反向传播公式有：
$\delta^{L} = a^{(L)} - y^{(L)}$
$\delta^{l} = (\Theta^{(l)})^T\delta^{(l + 1)} .* {g}’(z^{(l)})$

神经网络有点黑盒的感觉，上面的公式推导并不是太难。为什么这样子可行，不是太容易理解。从之前的例子来看就是更多的节点构建的模型可以更复杂，更容易拟合数据。

支持向量机

支持向量机要从逻辑回归说起，对于单项的损失而言，下图中上面是单项的损失函数，下面是对应的函数曲线。

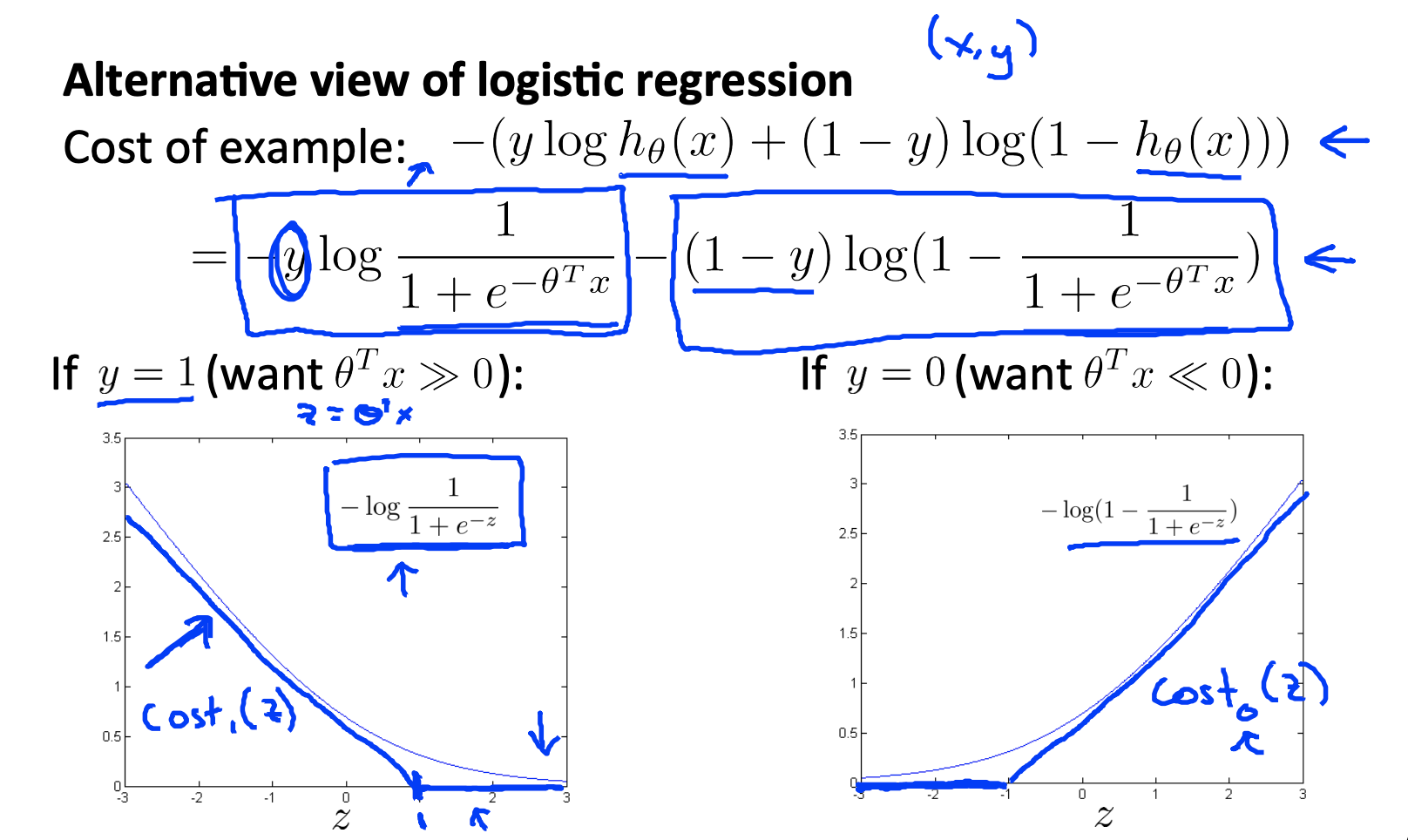
直观上看就是我们使用曲线下面的直接来替换原来的函数，我们令

$$\begin{aligned}
cost_1(\theta^Tx^{(i)}) = max(0, K(1 - z))
cost_0(\theta^Tx^{(i)}) = max(0, K(1 + z))
\end{aligned}$$

然后用 $cost_1(\theta^Tx^{(i)})$ 和 $cost_0(\theta^Tx^{(i)})$ 分别替换 $(-logh_{\theta}(x^{(i)})$ 和 $(-log(1 - h_{\theta}(x^{(i)}))$ 得到新的损失函数

$$J(\theta) = C\frac{1}{m}\sum_{i = 1}^{m}\left [ y^{(i)}cost_1(\theta^Tx^{(i)}) + (1 - y^{(i)})cost_0(\theta^Tx^{(i)}) \right ] + \frac{1}{2}\sum_{i = 1}^{n}\theta_j^2$$

这儿的 C 和 $\lambda$ 一样，可以看出当 C 值比较大时，为了取得最小值，损失函数必须为 0， 也就是说当 y 为 1 时，$\theta^Tx^{(i)} >= 1$，当 y 为 0 时，$\theta^Tx^{(i)} <= -1$

SVM 又称为大间隔分类器，因为当 C 比较大的时候，决策边界离正负样本的距离都比较远。它的数学原理是这样子的：$\theta^T >= 1$ 也就是向量的内积，因为惩罚参数项当 $\theta$ 值变得越来越小时，为了使内积满足 $\theta^Tx^{(i) >= 1$，根据 $\theta^T \dot x^{(i) = \left | \theta \right | \left | x^{(i)} \right | cos\alpha$ 夹角必须尽可能的小， 也就是必须使得 $\theta$ 尽可能的与数据集尽量在同一方向，表现出来的就是与决策边界正交。

核函数

对于非线性分界线的情况，比如只有两个特征 $x_1$ 和 $x_2$, 我们可以扩展我们的特征，假设函数可能是

$\theta_0 + \theta_1 x_1+ \theta_2 x_2 + \theta_3 x_1x_2 + \theta_4 x_1^2 + \theta_5 x_2^2 + … > 0$

我们可以根据给定的 x 和 地标 $l^{(1)} l^{(2)} l^{(3)}$ 计算出新的特征 f

$f_1 = similarity(x, l^{(1)}) = exp(-\frac{\left | x - l^{(1)} \right |^2}{2\sigma ^2})$

这个相似度函数又叫高斯核函数，在 x 与 $l^{(1)}$ 比较接近时取得 1，较远时为 0。

而 $l^{(1)} l^{(2)} l^{(3)}$ 的选择则是 $l^{(1)}=x^{(1)}； l^{(2)}=x^{(2)}； l^{(3)}=x^{(3)}$。感觉上将原来的 n 维的 $x^{(i)}$扩展为 m 维的 $f^{(i)}$。在模型训练中的成本函数也就变为

$$J(\theta) = C\frac{1}{m}\sum_{i = 1}^{m}\left [ y^{(i)}cost_1(\theta^Tf^{(i)}) + (1 - y^{(i)})cost_0(\theta^Tf^{(i)}) \right ] + \frac{1}{2}\sum_{i = 1}^{m}\theta_j^2$$

SVM 参数选择

Large C: Lower bias high variance 训练数据偏差更小，可能过拟合。
Small C: Higher bias low variance

Large $\sigma^2$ $f_i$ 变化更缓慢，Higer bias low variance
Small $\sigma^2$ $f_i$ 更陡峭， Lower bias high variance 意味着只有当两个向量非常相近时才认为相似，训练出的参数可能过拟合。

逻辑回归和 SVM 的选择

如果 n 非常大（相当于 m），逻辑回归或者 SVM 没有核函数

如果 n 比较小，m 适中， SVM + 高斯核函数

如果 n 小 m 比较大，添加更多特征，使用逻辑回归或者没有核函数的 SVM

非监督学习

聚类

非监督学习的训练集 ${x^{(1)},x^{(2)},x^{(3)},…,x^{(m)}}$ 要分类数为 K
K-means 算法比较直观：
首先随机初始化 K 个 cluster centriods $\mu_1, \mu_2,…,\mu_K$，之后重复以下步骤：

1. 对所有的 m 个数据： $c^{(i)}$ 设置为离 $x^{(i)}$ 最近的 cluster centriods 索引
2. 对所有的 K 个： 对索引为 k 的点求平均，然后设置为新的 $\mu_k$

对应的损失函数

$$J(c, \mu) = \frac{1}{m}\sum_{i=1}^{m}\left | x^{(i)} - \mu_{c^{(i)}} \right |^2$$

这个算法也和随机初始化时选择的位置有关，所以一般会重复多次找到效果最好的一次。

至于 K 的选择，没有什么更好的办法，所谓的 Elbow 方法就是慢慢增加 K 一直到不能看到明显变化。

维度规约

维度规约顾名思义，将原来高维度的数据降维，同时要保持数据大部分的特征。比如降低到二维可以可视化呈现，或者进行数据压缩。

Principal Component Analysis(主成分分析) 算法
将 n 维数据降低到 k 维

1. 计算 方差矩阵
   $$\Sigma = \frac{1}{m}\sum_{i = 1}^{n}(x^{(i)})(x^{(i)})^T$$
2. 计算矩阵的 eigenvectors
   $$[U, S, V] = svd(Sigma)$$

这部分只讲了怎么计算，没有解释为什么，涉及到的线代知识后面再补上

异常检测

这个涉及到大数定理和高斯正态分布，简单来说已有的数据符合高斯正态分布，我们计算出正态分布的 $\mu$ 和 $\sigma^2$ 对于给定的新数据，计算分布的概率。如果概率小于某个值则认为是异常。

异常检测其实和监督学习有点像，只是一般来说异常监测的正例数目非常小而且没有一定的特征，比如是否是诈骗邮件。

大规模机器学习

简单思路：先用小部分数据训练模型，逐渐增加数据规模。
在线的机器学习，并不保留数据，根据新来的直接数据更新参数。
MapReduce 不再多说。

OCR 例子

视频的最后介绍了一个机器学习的常见应用： OCR。整个流程有：文字检测；字符切割；字符分类。检测的方法没有很好的办法就是滑动窗口，移动窗口逐个检测，逐渐调整窗口大小，字符切割也需要用到滑动窗口。实际感觉这些流程处理起来也不简单。最后还介绍了人工制造数据，比如通过反转图片，扭曲图片来生成新的数据。

小结

整个视频涉及到的数学知识并不多，而且学习之后的课程练习也可以实实在在的感受到确实可以用来解决一些问题，总体来说确实比较适合的同学吧。